PYET-MC

pyet_logo

A library to model energy transfer between lanthanide ions

Get in contact or follow research related to this project

Project Overview

Collection of tools for modelling the energy transfer processes in lanthanide-doped materials.

Contains functions for visualising crystal structure around a central donor ion, subroutines for nearest neighbour probabilities and monte-carlo based multi-objective fitting for energy transfer rates. This package aims to streamline the fitting process while providing useful tools to obtain quick structural information. The core function of this library is the ability to simultaneously fit lifetime data for various concentrations to tie down energy transfer rates more accurately. This allows one to decouple certain dataset features, such as signal offset/amplitude, from physical parameters, such as radiative and energy transfer rates. This is all handled by a relatively straightforward API wrapping the Scipy Optimise library. This library is based on the scripts initially written for studying multi-polar interactions between samarium ions in KY₃F₁₀ [1]

Road Map

~~Migrate a lot of the plotting functionality to Plotly and wrap it in a matplotlib-like GUI. This work has started, an example of this transition can be found here & here.~~ ✅
~~Update structure figures to use Jmol colour palette. Correct atom colours are coming soon!~~
~~Move compute-heavy / memory-intensive functions to Rust for better performance.~~
Add more interaction types, e.g., cooperative energy transfer and other more complex energy transfer processes.
Add geometric correction factors and shield factors for various crystal structures and ions [2].
Add alternative to Monte Carlo methods e.g. the shell model(performance vs accuracy tests required). If successful, the shell model could improve performance greatly [3,4].
~~Move docs to MDbook for continuous integration.~~
Optional open-source database where results can be stored, retrieved, and rated based on data quality and fit, much like the ICCD crystallography database.
Add more tests; this will be important as the project grows and other users want to add features.

Installation

Installation Currently, pyet is not on the PyPI package repository; this will be the case until this project is more stable. It is still a work in progress. However, if you do wish to use pyet in its current form, it is as simple as the following:

Setup a new Python virtual environment (I recommend Conda, via miniforge) and specify Python 3.11. The conda recomendation stems from the depedencies of this project, outlined below.

conda create --name 'name of your env' python=3.11

Activate this virtual environment with "conda activate 'name of your env'". This ensures the package doesn't overwrite any of your existing Numpy/Scipy Python libraries There are two options to install this package either through the provided wheels or building from source. Building from source will require the rust compiler and maturin to be installed. The most straightforward way is to do, simply download the latest release build from the GitHub repository.

then after activating your conda or environment manager of your choice simply

pip install pyet-mc

If you encounter any issues, this may be due to pymatgen recommending you install its numpy and matplotlib dependencies via conda first.

conda install numpy matplotlib

pyet should now successfully be installed!

To test that this was successful, create a new Python file (wherever you would like to use pyet-mc, not from within the pyet-mc source code). Try to import pyet; assuming no error messages appear, pyet has been successfully installed in your virtual environment

from pyet_mc.structure import Structure, Interaction
from pyet_mc.fitting import Optimiser, general_energy_transfer
from pyet_mc.pyet_utils import Trace, cache_reader, cache_list, cache_clear
from pyet_mc.plotting import Plot

Building From Source

If you prefer, you can build from source.

Firstly, ensure you have the rust toolchain and maturin installed. You can install it directly into your virtual environment you plan to use with this project by running:

conda activate "name of your env"
git clone git@github.com:JaminMartin/pyet-mc.git && cd pyet-mc 
maturin develop --release

The location of this does not matter as it is installed into the virtual environment.

Generating a structure & plotting

Note a complete example of the following code can be found here

Generating a structure & plotting

Firstly, a .cif file must be provided. How you provide this .cif file is up to you! We will take a .cif file from the materials project website for this example. However, they also provide a convenient API that can also be used to provide .cif data. It is highly recommended as it provides additional functionality, such as XRD patterns. Information on how to access this API can be found here: https://next-gen.materialsproject.org/api. We can create our structure with the following code. However, this may differ if you are using the materials project API. It is also important to ensure your .cif file is using the conventional standard.

KY3F10 = Structure(cif_file= 'KY3F10.cif')

We then need to specify a central ion, to which all subsequent information will be calculated in relation to. It is important to note, we must specify the charge of the ion as well.

KY3F10.centre_ion('Y3+')

This will set the central ion to be a Ytrrium ion and yield the following output:

central ion is [-5.857692   -5.857692   -2.81691722] Y3+
with a nearest neighbour Y3+ at 3.914906764969714 angstroms

This gives us the basic information about the host material. Now we can request some information! We can now query what ions and how far away they are from that central ion within a given radius. This can be done with the following:

KY3F10.nearest_neighbours_info(3.2)

Output:

Nearest neighbours within radius 3.2 Angstroms of a Y3+ ion:
Species = F, r = 2.386628 Angstrom
Species = F, r = 2.227665 Angstrom
Species = F, r = 2.386628 Angstrom
Species = F, r = 2.227665 Angstrom
Species = F, r = 2.386628 Angstrom
Species = F, r = 2.227665 Angstrom
Species = F, r = 2.227665 Angstrom
Species = F, r = 2.386628 Angstrom

We can plot this if we like, but we will increase the radius for illustrative purposes. We can use the inbuilt plotting for this.

if __name__ == "__main__":
    fig1 = KY3F10.structure_plot(radius = 5)  
    fig1.show()

Which yields the following figure:

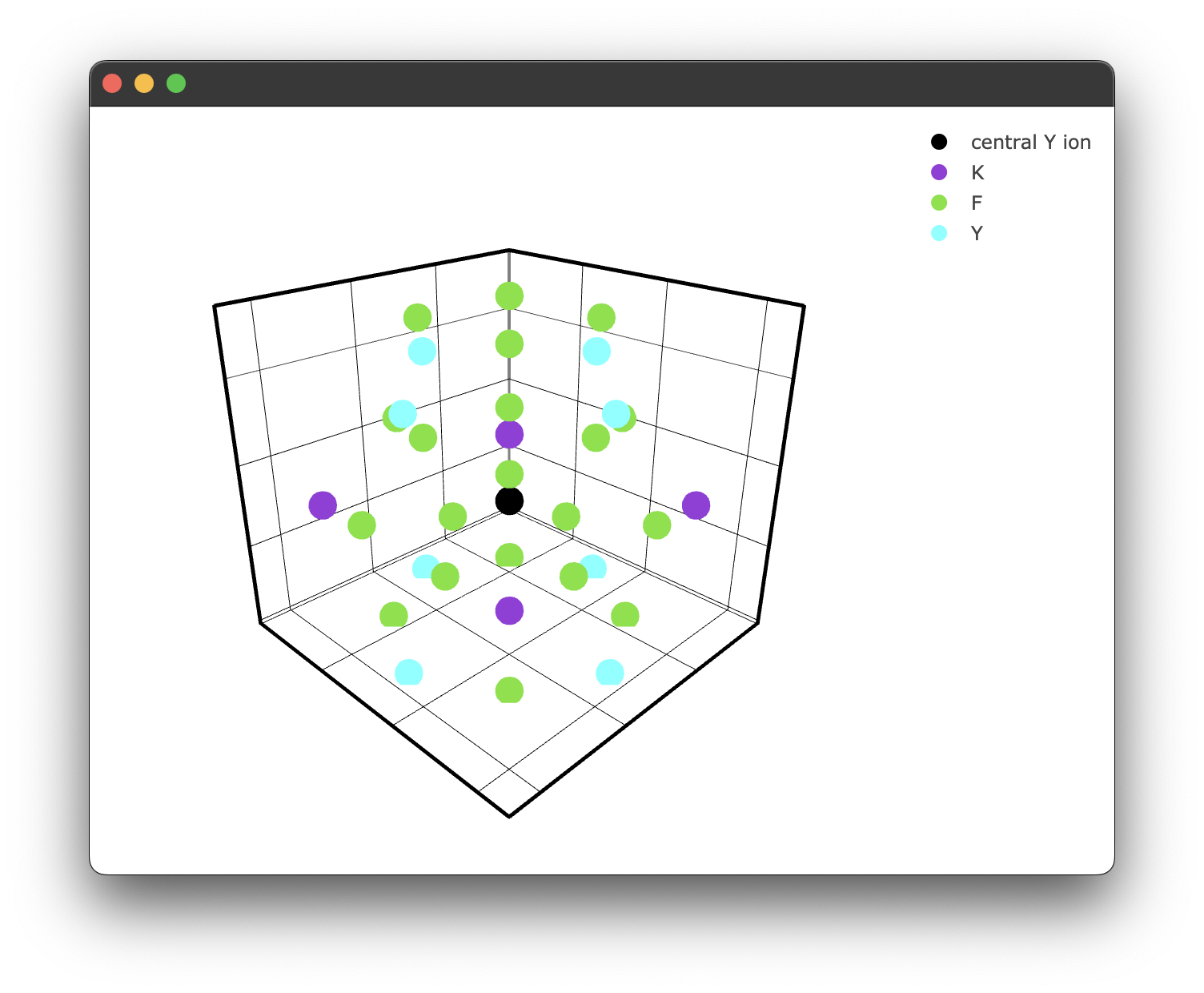
example lifetime and energy transfer fitting plot

It's worth noting here briefly that due to the way the PyWebEngine App is being rendered using the multiprocessing library, it is essential to include the if __name__ == "__main__": block. Unfortunately, until a different backend for rendering the Plotly .html files that also supports javascript this has to stay. We can also specify a filter only to show ions we care about. For example, we may only care about the fluoride ions.

if __name__ == "__main__":
  filtered_ions = ['F-', 'K+'] #again, note we must specify the charge!

  fig2 = KY3F10.structure_plot(radius = 5, filter = filtered_ions)  
  fig2.show()

This gives us a filtered plot:

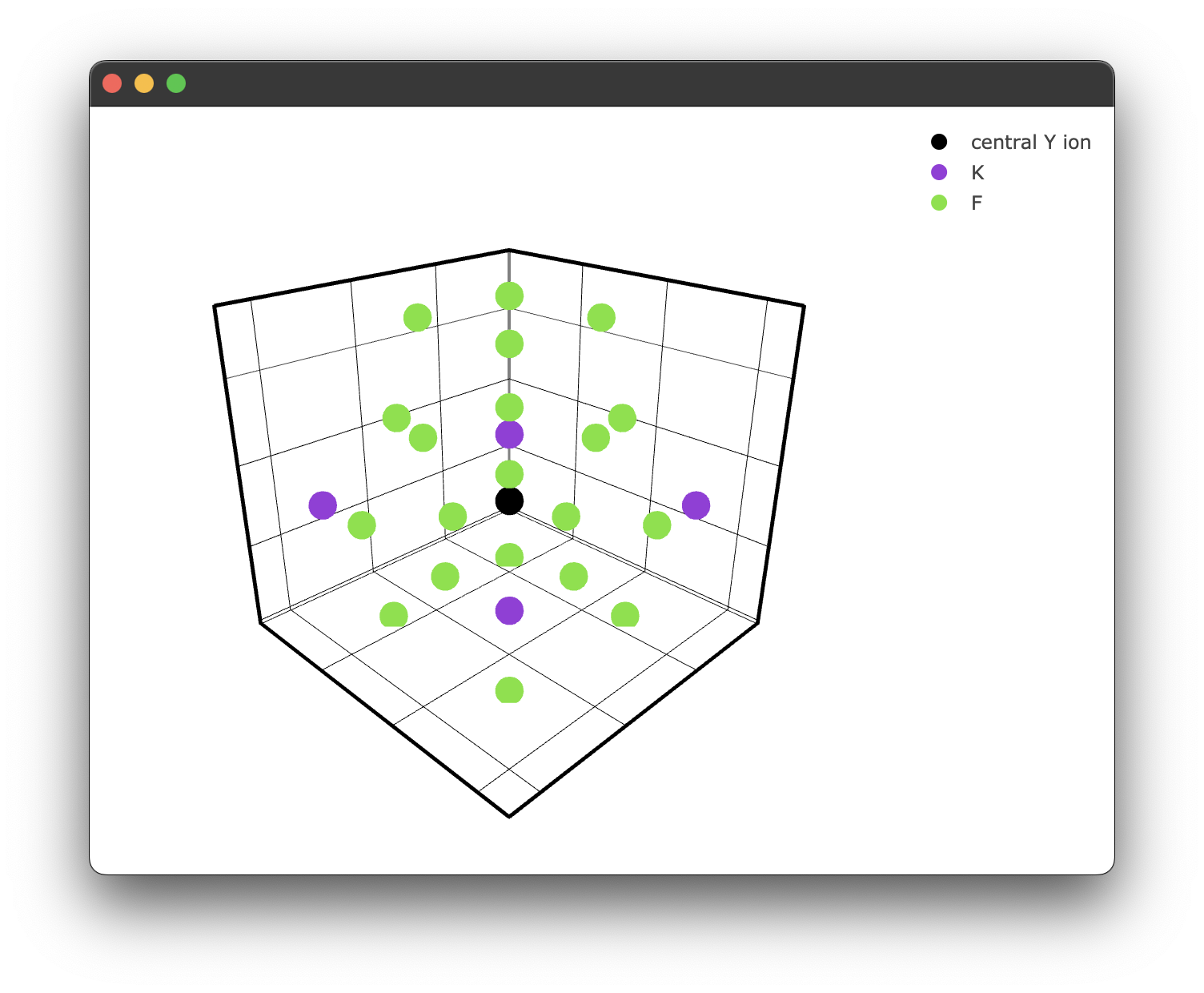
example lifetime and energy transfer fitting plot

Energy transfer models

The energy transfer process can be modelled for a particular configuration of donor and acceptor ions with the following exponential function here $t$ is time, $γ_{r}$ is the radiative decay rate, and $γ_{t r, j}$ is the energy transfer rate for this configuration. Assuming a single-step multipole-multipole interaction (currently, the only model implemented), $γ_{t r, j}$ may be modelled as a sum over the transfer rates to all acceptors $γ_{t r, j}$ takes the form:

$γ_{t r, j} = C_{cr} i \sum (\frac{R _{0}}{R _{i}})^{s}$ $I_{j} (t) = e^{- (γ_{r} + γ_{t r, j}) t}$ Here $R_{i}$ is the distance between donor and acceptor, $C_{cr}$ is the energy-transfer rate to an acceptor at $R_{0}$ the nearest-neighbour distance, and $s$ depends on the type of multipole-multipole interaction ( $s$ = 6, 8, 10 for dipole-dipole, dipole-quadrupole and quadrupole-quadrupole interactions respectively). The term $\sum_{i} (\frac{R _{0}}{R _{i}})^{s}$ forms the basis of our Monte Carlo simulation; we will refer to this as our interaction component. The lifetime for an ensemble of donors can be modelled by averaging over many possible configurations of donors and acceptors:

$I (t) = \frac{1}{n} j = 1 \sum n e^{- (γ_{r} + γ_{t r, j}) t}$

Where $n$ is the number of unique random configurations. We can also define an average energy transfer rate $γ_{a v}$ defined as: $\frac{1}{n} j = 1 \sum n γ_{t r, j}$ This is a useful value for comparing hosts at a similar concentration.

Modelling energy transfer processes

Note: Currently, only one energy transfer process has been implemented, so this section may be subject to change in future releases.

Consider the crystal structure we previously generated. We wish to "dope" that structure with some lanthanide ions randomly around some central donor ion. We will replace our previously defined "central yttrium atom" with a samarium. We will then randomly (based on the concentration of the dopant in the crystal) dope samarium ions around this central samarium ion. This step must be performed many times to "build up" many random unique samarium-samarium donor-acceptor configurations. When the number of random configurations is large enough, this should accurately represent a physical crystal sample. This is the Monte-Carlo aspect of our energy transfer analysis.

To generate our random samples, we utilise the interaction class. This class takes in our structure class and provides additional methods for calculating our interaction components and more specific plotting methods for doped crystals. We can enact this class simply by passing our structure to the interaction class:

crystal_interaction = Interaction(KY3F10)

coords = crystal_interaction.distance_sim(radius=10, concentration = 15, dopant='Sm3+')

This returns a list of radial distances in angstroms of the dopant samarium ions about the central samarium donor ion.

[8.28402747 7.17592429 7.17592429 9.33368811 8.28402747 4.30030493
 8.28402747 7.17592429 9.33368811 7.17592429 3.98372254 8.28402747]

We can also take a more detailed look at what has happened by calling

print(coords.filtered_coords)

           r       theta           phi species
0   7.175924  115.071364 -1.156825e+02       Y3+
1   7.175924  115.071364 -1.543175e+02       Y3+
2   8.284027   90.000000 -1.350000e+02       Y3+
3   7.175924   66.886668 -1.525658e+02       Y3+
4   7.175924   66.886668 -1.174342e+02       Y3+
5   9.192125  109.317471 -1.800000e+02       Y3+
6   5.861968   92.188550 -1.800000e+02       Y3+
7   9.333688  162.434187 -1.800000e+02       Y3+
8   8.284027  135.000000  1.800000e+02      Sm3+
9   7.175924  115.071364  1.156825e+02      Sm3+
10  7.175924  115.071364  1.543175e+02       Y3+
11  4.300305  135.000000 -1.800000e+02       Y3+
12  3.983723   45.000000 -1.800000e+02       Y3+
13  7.175924   66.886668  1.525658e+02      Sm3+
14  9.333688   72.434187 -1.800000e+02      Sm3+
15  8.284027   45.000000 -1.800000e+02       Y3+
16  9.192125   19.317471 -1.800000e+02       Y3+
17  8.284027   90.000000  1.350000e+02       Y3+
18  7.175924   66.886668  1.174342e+02       Y3+
19  9.192125  109.317471 -9.000000e+01       Y3+
20  5.861968   92.188550 -9.000000e+01       Y3+

As we can see, some of the yttrium ions have been replaced by samarium ions, as expected. We can also plot this to see what is happening visually; the interaction class has similar plotting functionality.

if __name__ == "__main__":
    fig3 = crystal_interaction.doped_structure_plot(radius=7.0, concentration = 15.0 , dopant = 'Sm3+' , filter = ['Y3+','Sm3+'])
    fig3.show()

yielding the following figure:

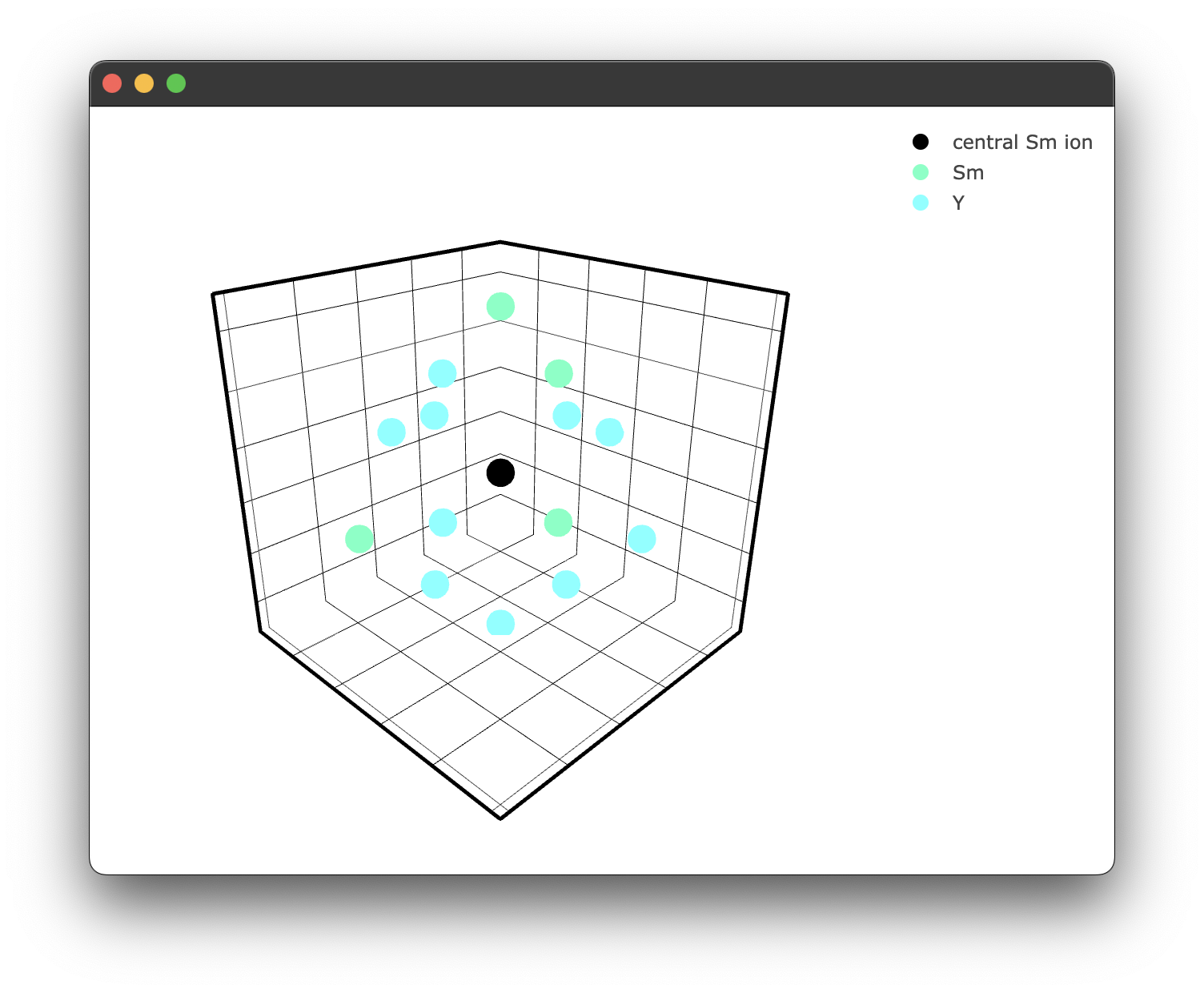
example lifetime and energy transfer fitting plot

We can now calculate our interaction component for each random doping configuration. This is handled by the sim method, which currently is referred to as sim_single_cross as it is the only implemented method at the time of writing. However, it is possible to add your own by wrapping 'distance_method' described above for cooperative processes, for example.

interaction_components2pt5pct = crystal_interaction.sim_single_cross(radius=10, concentration = 2.5, interaction_type='DQ', iterations=20)

The sim method takes a radius, concentration, interaction type and number of iterations. The interaction type is given by a two-letter code, i.e. 'DQ' equals dipole-quadrupole. We will need more iterations than just 20 for fitting, closer to 50,0000. If we rerun this now with 50,0000 iterations, we get the following response:

file found in cache, returning interaction components

This is because I have already run this command, which has been cached. See the notes on caching here. The sim returns a Numpy array of interaction components that matches the number of iterations and will be utilised in our fitting process next!

We can then generate another set of interaction components for a 5% doped sample simply by changing the concentration

interaction_components5pct = crystal_interaction.sim_single_cross(radius=10, concentration = 5, interaction_type='DQ', iterations=50000)

The crystal interaction simulation can also accept the boolean flag intrinsic = True; this uses a modified formulation of the interaction components in the form $γ_{t r, j} = C_{cr} i \sum (\frac{1}{R _{i}})^{s} .$

This gives us the energy transfer rate ( $C_{cr}$ ) or average energy transfer rate ( $γ_{a v}$ ) in terms of a dopant ion 1 Å from the donor ion. The relevance of this is for work regarding an intrinsic energy rate. It is set to false by default as it is not as relevant at this stage; however, in future, it may be of interest.

Adding your own interaction model

Adding your own model should be relatively straightforward. In the above code, we call the: .sim_single_cross method. You can add a different interaction method simply by defining a new function that can inherit the properties of the Interaction class e.g.

def sim_cooperative_energy_transfer(self, arg1, arg2, argn):
    # your code here # or you could write in in C or Rust and import it here

crystal_interaction = Interaction(KY3F10) # as shown before 
crystal_interaction.sim_cooperative_energy_transfer = sim_cooperative_energy_transfer

We can then use this method as the above default example.

A note on caching

As these calculations can be quite time-consuming for large iterations, and for said large iterations, the difference between runs should be minimal, caching was implemented to speed up subsequent runs.

When first used, pyet will create a cache directory. All interaction simulations will cache their interaction components along with info regarding the simulation conditions in JSON format. The generated JSON file is named in the following convention:

process_radius_concentration_interactiontype_iterations_intrinsic_timedatestamp.json

Resulting in a file name:

singlecross_10_2pt5_DQ_1000_intrinsic_False_20240827080449.json

When generating interaction components it also takes note of the .cif file used, that way you can have multiple interaction components of identical parameters, but from different crystal structures.

We can query and return the interaction components of the JSON file with the following code:

from pyet_mc.pyet_utils import cache_reader, cache_clear, cache_list

interaction_components2pt5pct = cache_reader(process = 'singlecross', radius = 10 , concentration = 2.5 , iterations = 50000 , interaction_type = 'DQ', intrinsic = False, sourcefile = "KY3F10.cif")
interaction_components5pct =  cache_reader(process = 'singlecross', radius = 10 , concentration = 5 , iterations = 50000 , interaction_type = 'DQ', intrinsic = False, sourcefile = "KY3F10.cif")

If what you have specified is not found in the cache, there will be a console log such as this:

File not found, check your inputs or consider running a simulation with these parameters

This will also return a None type, which must be handled accordingly, such as using a Python match statement. However, most likely you won't run into this as the Interaction.sim_single_cross() method implements this before it runs anyway. If the query does return, it will return a Numpy array of our interaction components. In that case, the following is also displayed:

file found in cache, returning interaction components

Following a major update to pyet-mc, it is also recommended that you clear the cache in the event a bug is discovered in the existing code. This will be highlighted in any release notes.

This can be done using:

cache_clear()

This will prompt you if you are sure you would like to delete the cache.

Are you sure you want to delete all the cache files? [Y/N]?

You can also specify a file of a given simulation configuration, as was done above. In the event, you may have made a mistake and forgot to change a .cif file etc. It happens to the best of us...

If you want to know the status of your cache, you can also use the cache list to get the details, including file names and sizes. Like cache_clear(), a simple command is all you need!

cache_list()

#======# Cached Files #======#
[0] singlecross_10_2pt5_DQ_1000_intrinsic_False_20240827080449.json (18017 bytes), Source file: KY3F10.cif, Date created: 2024-08-27T08:04:49.396355
[1] singlecross_10_5pt0_DQ_1000_intrinsic_False_20240827080449.json (20593 bytes), Source file: KY3F10.cif, Date created: 2024-08-27T08:04:49.622935
Total cache size: 0.04 MB
Run "cache_clear()" to clear the cache
#============================#

You can then delete a selected file like so:

cache_clear(0)
File to delete: singlecross_10_2pt5_DQ_1000_intrinsic_False_20240827080449.json Source file: KY3F10.cif, Date created: 2024-08-27T08:04:49.396355
Are you sure you want to delete this file? [Y/N]
y
Deleted file: singlecross_10_2pt5_DQ_1000_intrinsic_False_20240827080449.json

Fitting experimental data to energy transfer models

The following covers the core aspect of this library, the fitting. The core purpose of this is to make the fitting of multiple lifetime data sets as simple as possible. It also allows for each dataset to contribute to a single fit rather than running multiple fits for different concentrations.

General Fitting

Recalling our two dipole-quadrupole datasets previously for 2.5% and 5% doping, respectively, If you do not have these generated interaction components, please refer to modelling energy transfer processes. We can use them to generate some artificial data given some additional parameters. For this particular model, we must provide it with four additional parameters: an amplitude, cross-relaxation rate ( $C_{cr}$ ), a radiative decay rate, and horizontal offset.

#specify additional constants (the time based constants are in ms^-1)
const_dict1  = {'amplitude': 1 , 'energy_transfer': 500, 'radiative_decay' : 0.144, 'offset':0}
const_dict2  = {'amplitude': 1 , 'energy_transfer': 500, 'radiative_decay' : 0.144, 'offset': 0}

Note the units used here, the energy transfer and radiative rates are given in $ms^{- 1}$ , it is more common to have these in $s^{- 1}$ , however here we are using $ms^{- 1}$ for the purpose of generating data with a nice time scale. Now we can generate some synthetic data and plot it:

if __name__ == "__main__":
    # generate some random data
    time = np.arange(0,21,0.02) #1050 data points 0 to 21ms
    #Generate some random data based on our provided constants and time basis
    data_2pt5pct = general_energy_transfer(time, interaction_components2pt5pct, const_dict1)
    data_5pct = general_energy_transfer(time, interaction_components5pct, const_dict2)
    #Add some noise to make it more realistic
    rng = np.random.default_rng()
    noise = 0.01 * rng.normal(size=time.size)
    data_2pt5pct = data_2pt5pct + noise
    data_5pct = data_5pct + noise

    #Plotting
    fig4 = Plot()
    fig4.transient(time, data_2pt5pct)
    fig4.transient(time, data_5pct)
    fig4.show()

which gives the following result:

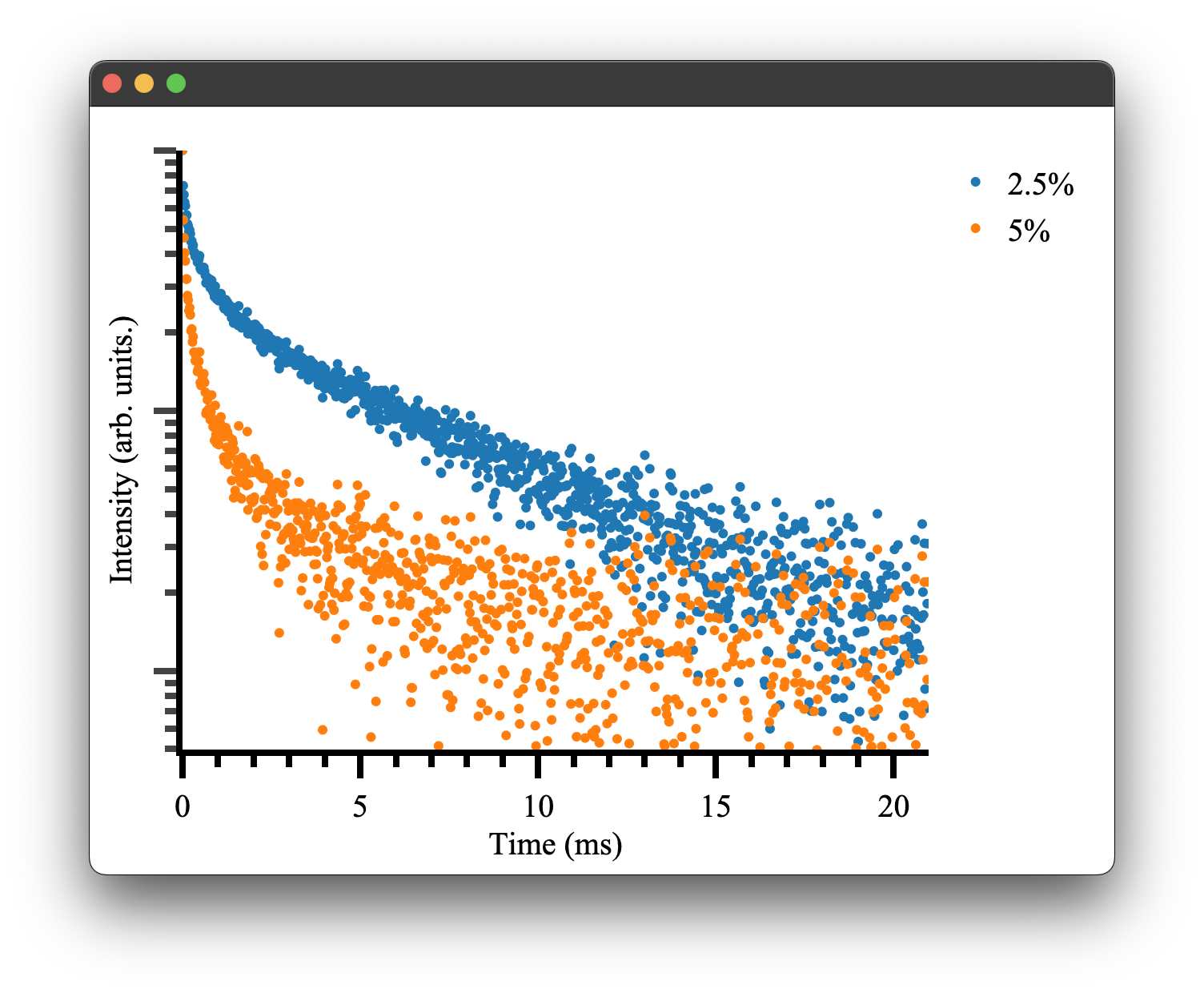
as we would expect! To see more details on how plotting and the Plot.transient() method works please see the plotting documentation.

We can attempt to fit the parameters initially used to generate this data. Pyet provides a wrapper around the scipy.optimise library to simultaneously fit multiple data traces that should have the same physical parameters, e.g. our radiative cross-relaxation rates while allowing our offset and amplitude to vary independently.

We must first specify our independent and dependent parameters. We can achieve this by giving our variables either different (independent variables) or the same name (dependent variables)

params2pt5pct = ['amp1', 'cr', 'rad', 'offset1']
params5pct = ['amp2', 'cr', 'rad', 'offset2']

We then construct a trace object that takes our experimental data (e.g. signal, time), a label, and our interaction components

trace2pt5pct = Trace(data_2pt5pct, time,  '2.5%', interaction_components2pt5pct)
trace5pct = Trace(data_5pct, time, '5%', interaction_components5pct)

These objects and our list of variables can be passed to the optimiser for fitting.

opti = Optimiser([trace2pt5pct,trace5pct],[params2pt5pct,params5pct], model = 'default')

We choose the default model, which is our energy transfer model discussed above, and is the same model we used to generate the synthetic data. Note: This model can be supplemented with your own energy transfer model if it differs from the default model. We then give our model a guess. This can be inferred by inspecting the data or being very patient with the fitting / choice of the optimiser.

guess = {'amp1': 1, 'amp2': 1, 'cr': 100,'rad' : 0.500, 'offset1': 0 , 'offset2': 0}

As you can see, we only need to specify the unique set of parameters, in this case, six rather than eight total parameters. This will force the fitting to use the same cross-relaxation and radiative rates for both traces. This is what we would expect to be the case physically. The concentration dependence is handled by our interaction components. In a real experimental situation, you may only be able to have these parameters coupled if there is uncertainty in your actual concentrations. If your cross-relaxation parameters vary greatly, this is a good indication your concentrations used to calculate the interaction components are off.

Regardless, we can finally attempt to fit the data. We tell our optimiser to fit and give it one of the scipy.optimise methods and any other keywords, e.g. bounds or tolerance. The methods available all of those provided by scipy.optimise as well as dual-annealing, basinhoping and differential evolution. Details of their use can be found here here

res = opti.fit(guess, method = 'Nelder-Mead', tol = 1e-13)

This will return a dictionary of fitted parameters:

resulting fitted params:{'amp1': 0.9969421233991949, 'amp2': 0.9974422375924311, 'cr': 497.555275, 'rad': 0.146633387615, 'offset1': 0.0013088082858218686, 'offset2': 0.00020609427517915668}

Which is close to our given parameters and can be used to plot our final fitted results! There will also be some additional outputs regarding weightings, which is discussed here.

if __name__ == "__main__":
    fig5 = Plot()
    fig5.transient(trace2pt5pct)
    fig5.transient(trace5pct)
    #generate the data to show the fitted results 
    rdict = res.x #the dictionary within the result of the optimiser
    
    fit1 = general_energy_transfer(time, interaction_components2pt5pct, {'a': rdict['amp1'], 'b': rdict['cr'], 'c': rdict['rad'],'d': rdict['offset1']})
    fit2 = general_energy_transfer(time, interaction_components5pct, {'a': rdict['amp2'], 'b': rdict['cr'], 'c': rdict['rad'], 'd': rdict['offset2']})
    fig5.transient(time,fit1, fit=True, name = 'fit 2.5%')
    fig5.transient(time,fit2, fit = True, name = 'fit 5%')
    fig5.show()

Note the transient() method can take either a Trace or x, y data. the option fit = True will display the data in line mode rather than markers.

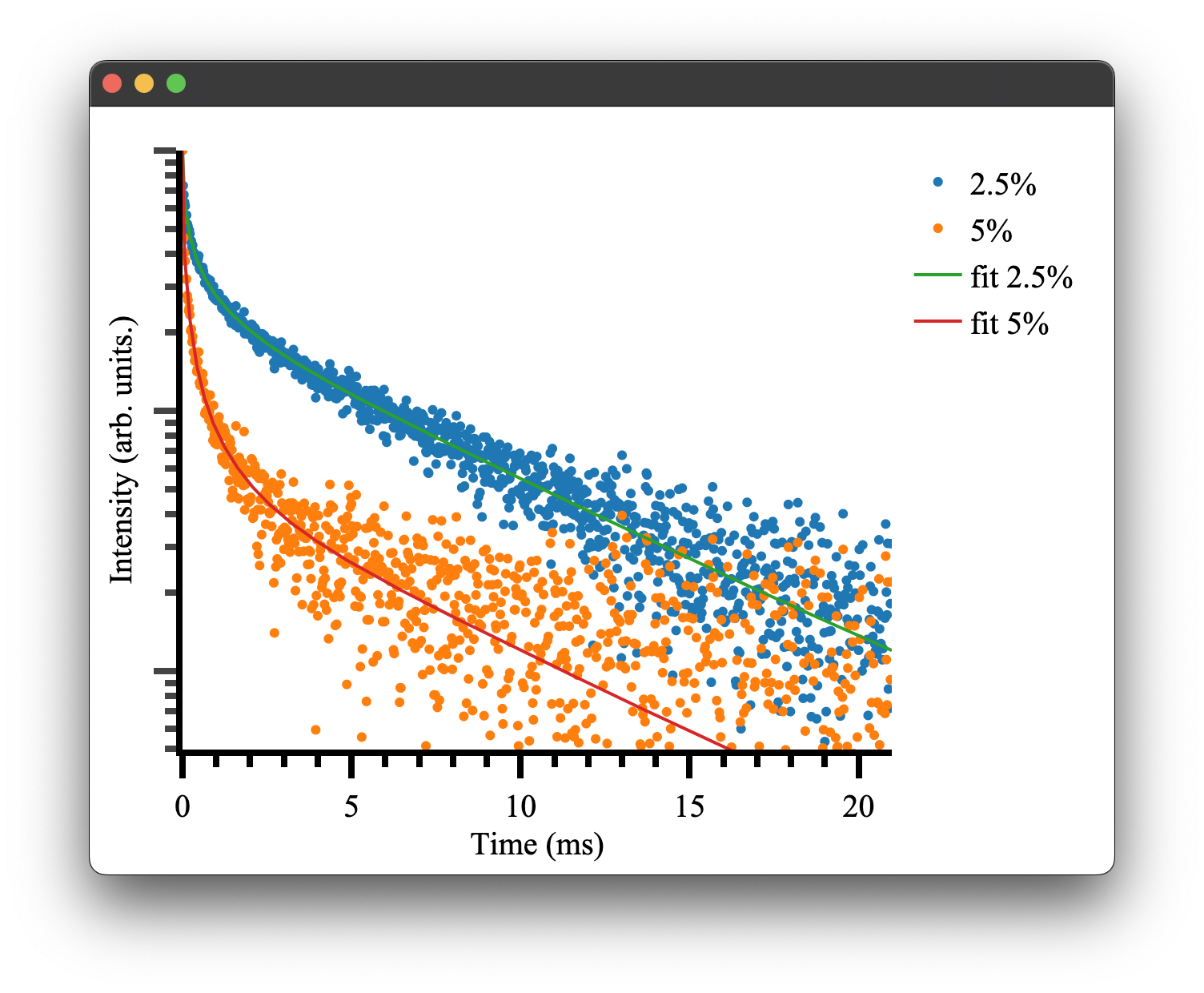
example lifetime and energy transfer fitting plot

Weighted Fitting

There is also the ability to have the fitting process weight each trace differently, as well as adjust the weighting of all traces when their length is not even. Take, for example, the case where we have two traces of different lengths. We can generate this as before with some slight modifications.

if __name__ == "__main__":
    from pyet.fitting import general_energy_transfer
    # generate some random data
    time_1050 = np.arange(0,21,0.02) #1050 data points 0 to 21ms
    time_525 = np.arange(0,21,0.04) #525 data points 0 to 21ms
    #Generate some random data based on our provided constants and time basis
    data_2pt5pct = general_energy_transfer(time_1050, interaction_components2pt5pct, const_dict1)
    data_5pct = general_energy_transfer(time_525, interaction_components5pct, const_dict2)
    #Add some noise to make it more realistic
    rng = np.random.default_rng()
    noise_1050 = 0.01 * rng.normal(size=time_1050.size)
    noise_525 = 0.01 * rng.normal(size=time_525.size)
    data_2pt5pct = data_2pt5pct + y_noise
    data_5pct = data_5pct + y_noise

This is much the same as before, but now we have two datasets of different lengths. If we try to fit this by trying to minimise the Residual Sum of Squares (RSS) (which this library uses) the fit would be intrinsically biased to the dataset of longer length. We could instead use the Mean Squared Error (MSE) to account for this, but MSE is subject to biasing from outlier data. Instead, we add an appropriate weighting to the smaller datasets so that their contribution is proportional to that of the longer dataset. This method requires the assumption all data sets have a similar variance, which is fair for these kinds of measurements with good signal quality and high numbers of averages. This gives us a Weighted Residual Sum of Squares (WRSS) implementation. This re-weighting of data is implemented as a default method in the fitting optimiser class. So if we re-ran the fit with this new dataset we would see this output during the fit:

the weights of the 2.5% trace has been adjusted to 1.0
the weights of the 5% trace has been adjusted to 2.0
['amp1', 'amp2', 'cr', 'rad', 'offset1', 'offset2']
Guess with initial params:{'amp1': 1, 'amp2': 1, 'cr': 100, 'rad': 0.5, 'offset1': 0, 'offset2': 0}
Started fitting...

This aims to compensate for the discrepancy in the number of data points. However, it can be turned off if it is not a desired feature simply by changing the instantiation of the optimiser to have auto_weighting set to False.

opti = Optimiser([trace2pt5pct,trace5pct],[params2pt5pct,params5pct], model = 'default', auto_weights = False)

There is also the ability to set a per-trace weighting to each Trace so that it intentionally biases the fitting process to try to either fit more or less to that data set. This is useful in the case where we have less than ideal data that we don't want to influence the fit or in the case we have ideal data that we want to fit more heavily to. To add a weighting factor to a trace it is as simple as declaring that when we create our Trace objects. Let's imagine the case where we want to weight our smaller dataset further for some contrived reason. We can simply add a weighting to that Trace. Note that by default the weighting is set to one.

trace2pt5pct = Trace(data_2pt5pct, time,  '2.5%', interaction_components2pt5pct)
trace5pct = Trace(data_5pct, time, '5%', interaction_components5pct, weighting = 5)

This would yield the following when fitting:

the weights of the 2.5% trace have been adjusted to 1.0
the weights of the 5% trace have been adjusted to 10.0
['amp1', 'amp2', 'cr', 'rad', 'offset1', 'offset2']
Guess with initial params:{'amp1': 1, 'amp2': 1, 'cr': 100, 'rad': 0.5, 'offset1': 0, 'offset2': 0}
Started fitting..

As you can see, the weighting has actually been adjusted to 10; this is due to the automatic re-weighting ensuring the weighting we provide is a weighting for equal datasets. If you don't want to use the automatic re-weighting but restain your weighting of 5 you can simply turn off automatic re-weighting as discussed.

There is no right or wrong way to implement these weights and should be addressed on a case-by-case basis, as they can heavily influence your fitted parameters.

Fitting Algorithms

Solvers

Plotting

The pyet-mc library comes with a built-in plotting library that 1. Provides a matplotlib style plotting wrapper for Plotly. It achieves this by rendering Plotly's html + js figures in a Qt5 WebEngine in a separate Python process. It also provides sensible defaults for plotting the spectra, lifetimes and crystal structures that may be of use to people not taking advantage of the fitting functionality of this library. Lastly, it features a unique plotting configuration method to make your code more readable at more readily checked between peers without clutter associated with plotting configuration.

Types of plots

Currently, there are three implemented plotting types. They are spectra, transient and structure_3d which are wrappers for Plotly's go.Scatter() and go.Scatter3d respectively. Where transient is specifically used for plotting lifetime data on a log scale.

Details of each plot type can be found here:

Spectra plots

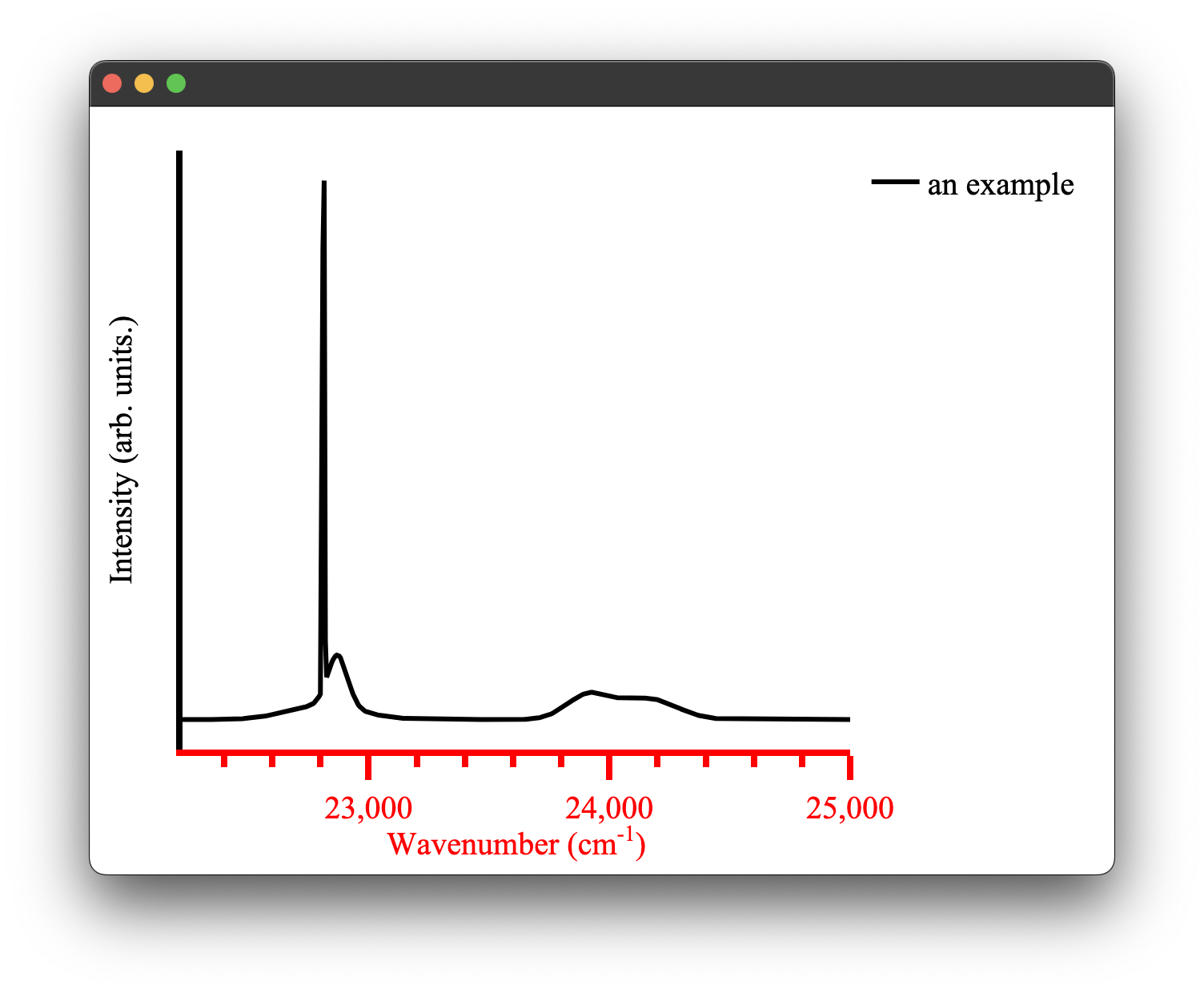
A spectra plot is a simple x,y plot of spectroscopic data with sensible defaults. It will for example, automatically find an appropriate major and minor tick spacing. It defaults to using wavenumbers as the x axis as that is what we commonly use in our research group. This can be easily overridden, however (see configuring plots) the goal is to be able to produce fast plots of spectra with sensible defaults that can be stylized to your tastes after. We can create a spectra plot simply with this code:

from pyet_mc.plotting import Plot
from pyet_mc.pyet_utils import random_spectra
if __name__ == "__main__":
    wavelengths = np.arange(400,450, 0.1) #generate some values between 400 and 450 nm
    wavenumbers, signal = random_spectra(wavelengths, wavenumbers=True)
    figure = Plot()
    figure.spectra(x, y, name = 'an example') #give the data a name for the legend
    figure.show()

which gives us the following figure:

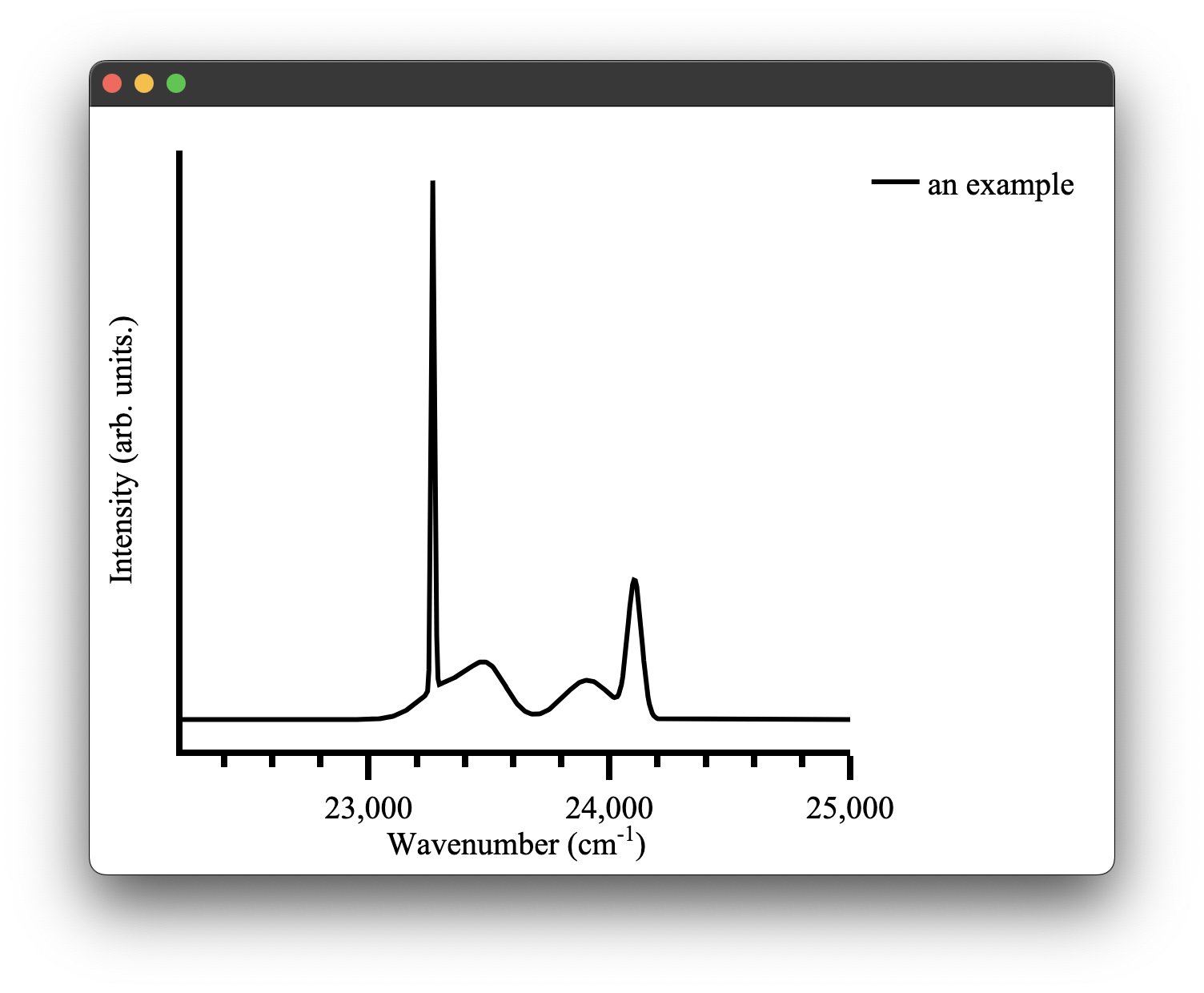
example spectra plot

Transient plots

The figures plotted using the transient plot type have been shown extensively in the section on fitting however it is worth discussing the purpose and limitations of this plot type.

The goal of this plot type is to quickly plot transients on an appropriate log scale for easy interpretation. It does, however, have its limitations - It may not correctly display this data, if so you may have to look at setting custom x,y axis limits. It then plots ~3 orders of magnitude on the y-axis and the x-axis limits are set from zero to the maximum value of your data. The x-axis label default is milliseconds; however, as was the case for the spectra plot, this can be easily reconfigured to an appropriate time base.

The transient plot type is designed to handle either x,y data as might be returned from the fitting process, for example, or it can take a Trace. This was to minimise code/data duplication. If you have defined a Trace for your data and given it a name, you can pass this in directly without having to worry about providing any y values.

Structure plots

The structure plots use Ploty's go.Scatter3d as their base. Unlike the previous two plot types, the structure plotting is handled by the structure3d plotting method, which is in turn wrapped by the Structure and Interaction plotting methods. These two methods leverage structure3d and its defaults to produce the structure plots we have seen earlier. It is however possible to bypass those structure plots if you don't have a .cif file or you want to write your own more general 3D plot.

To create a 3D plot without using a .cif file and Structure.structure_plot() or Interaction.doped_structure_plot() we simply need to use the methods we used for the spectra & transient plot types:

figure = Plot()

figure.structure_3d([0,1,2],[0,5,2],[0,1,5], name = 'Si')
figure.structure_3d([5,1,1],[2,0,1],[2,2,1], name='Y')
figure.show()

which gives us the following figure:

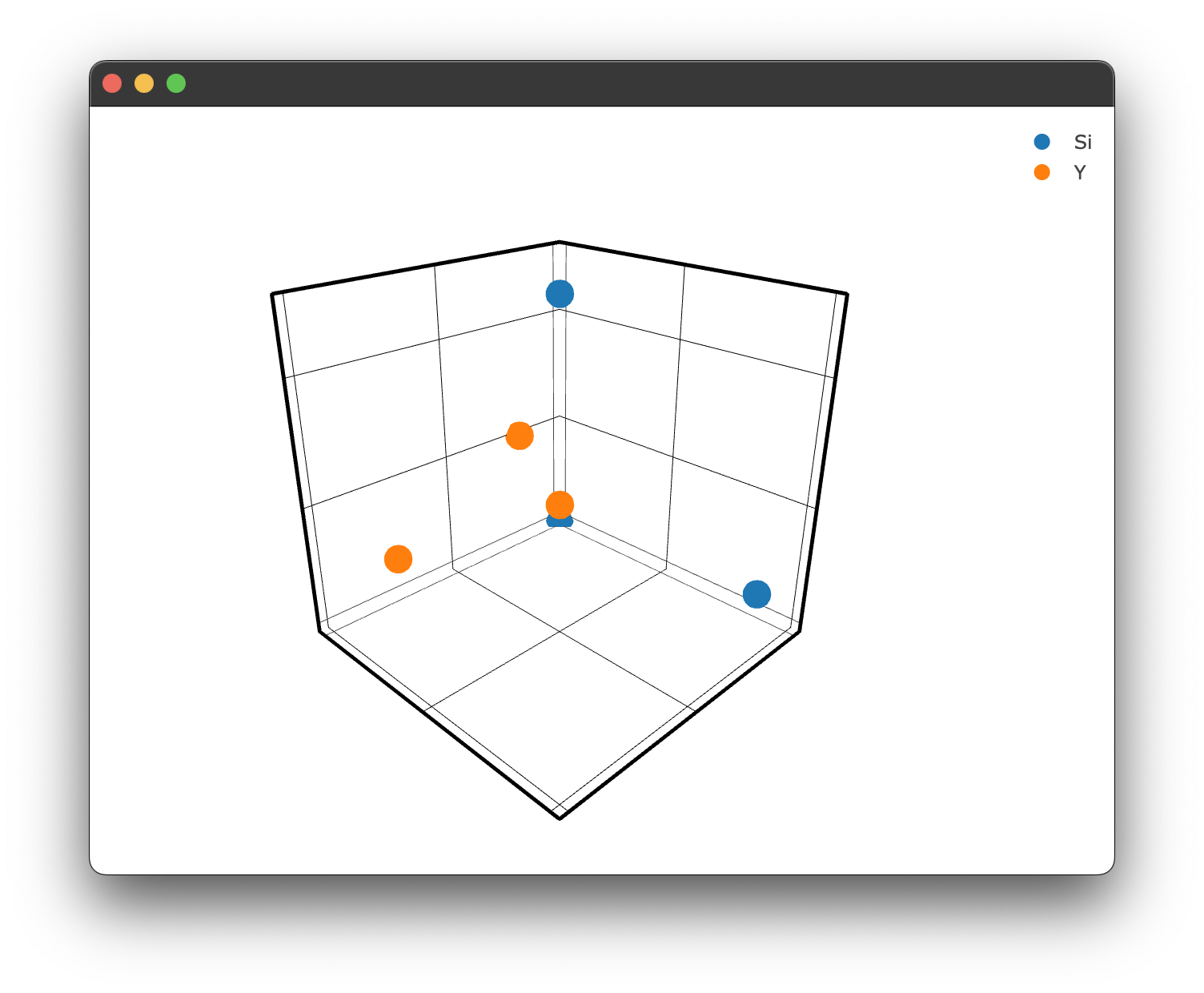
example structure3d plot

Configuring plots

There are a few ways to change the configuration of plots in pyet-mc. The most straight forward one is to directly pass layout arguments when creating our plot type. These layout arguments are just standard Plotly arguments and you can refer to their documentation for a full list of them. However, I shall show a few common examples.

The obvious one would be that the automatic x-axis range calculation of pyet-mc might not be quite what you want it to be. This can be easily changed by overwriting the defaults as we just discussed.

wavelengths = np.arange(400,450, 0.1) #generate some values between 400 and 450 nm
wavenumbers, signal = random_spectra(wavelengths, wavenumbers=True)
x_range = [23000,23500]
ticks = 50
figure = Plot(xaxis={'range': x_range,'dtick': 100})
figure.spectra(wavenumbers, signal, name = 'an example') #give the data a name for the legend
figure.show()

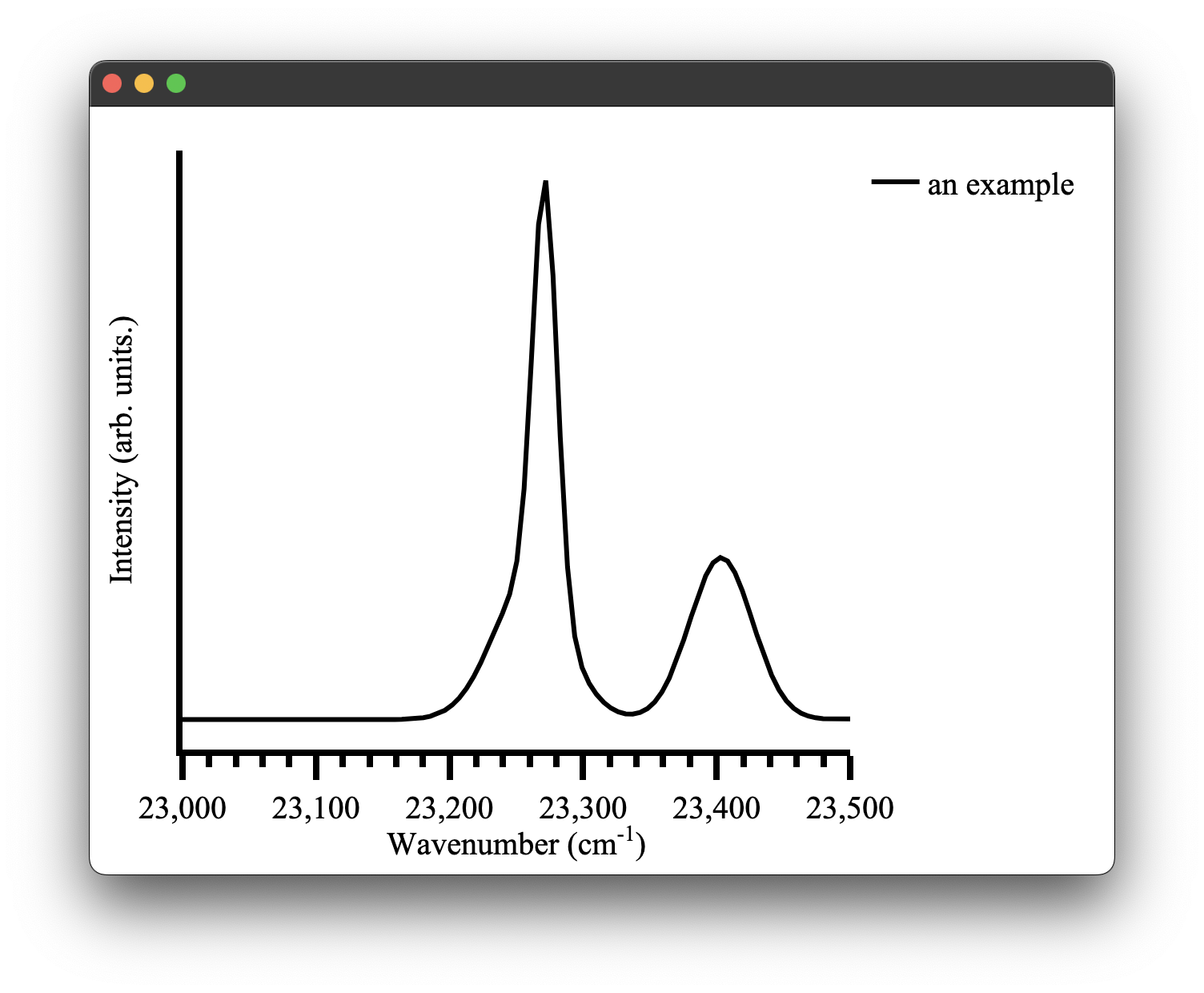
example directly passing layout elements

It is also easy to update the style of the data on the plot using a similar method:

wavelengths = np.arange(400,450, 0.1) #generate some values between 400 and 450 nm
wavenumbers, signal = random_spectra(wavelengths, wavenumbers=True)
x_range = [23000,23500]
ticks = 50
figure = Plot(xaxis={'range': x_range,'dtick': 100,})
figure.spectra(wavenumbers, signal, name='an example', mode='markers', marker={'color': 'red'}) 
figure.show()

example directly passing trace elements

While it is quite easy to specify a marker mode or colour for each dataset on a plot inline like the examples above, it becomes quite obtuse to do this for the plot layout configuration as there are far more options. This is greatly exemplified when you have multiple Python files plotting different sets of data but you want them to all have the same formatting, say for a thesis or publication. In pyet-mc a configuration method was introduced to simplify the layout configuration of Plotly plots. This is where all the default plot layouts are configured and, therefore, aren't hard-coded into the plotting functionality directly. When the plotting library is loaded it also loads this config file. Any arguments passed to the Plot() class overwrite it. However, it also means you can just directly modify this file and all your plots will be created with this layout by default!

The config file is a simple .toml file type, and the general layout of the plotting_congfig.toml file is:

[spectra_layout]
  title_text = ""
  showlegend = true
  title = ''
  margin = { l = 50, r = 50, t = 20, b = 70 }
  paper_bgcolor = "white"

  [spectra_layout.font]
    family = 'Times New Roman, monospace'
    size = 20
    color = 'black'

  [spectra_layout.xaxis]
    title = 'Wavenumber (cm<sup>-1</sup>)'
    exponentformat = 'none'
    showgrid = false
    showline = true
    tickmode = 'linear'
    ticks = 'outside'
    showticklabels = true
    linewidth = 4
    linecolor = 'black'
    ticklen = 15
    tickwidth = 4
    tickcolor = 'black'


    ...

where each of the three currently available plotting types has their layouts configured here. A full example of this file can be found in the src/pyet/plotting_config/ directory of the package on Github or wherever your Python package manager installed the library. You can directly edit the file there once the package has been installed. This is not the recommended way to provide a user-configured config file as it runs the risk of completely breaking the functionality of the library if you misconfigure it with no ability to fall back (unless, of course, you make a copy of the file or re-download it from this repo). Instead, you can use a pyet-utils function called load_local_config to load a local configuration from a specified directory. In this example we will change the x-axis colour scheme to red in our local config file.

[spectra_layout]
  title_text = ""
  showlegend = true
  title = ''
  margin = { l = 50, r = 50, t = 20, b = 70 }
  paper_bgcolor = "white"

  [spectra_layout.font]
    family = 'Times New Roman, monospace'
    size = 20
    color = 'black'

  [spectra_layout.xaxis]
    title = 'Wavenumber (cm<sup>-1</sup>)'
    exponentformat = 'none'
    showgrid = false
    showline = true
    tickmode = 'linear'
    ticks = 'outside'
    dtick = 50
    showticklabels = true
    linewidth = 4
    linecolor = 'red'
    ticklen = 15
    tickwidth = 4
    tickcolor = 'red'
    
    [spectra_layout.xaxis.minor]
      ticks = 'outside'
      ticklen = 7
      showgrid = false

    [spectra_layout.xaxis.tickfont]
      family = 'Times new roman, monospace'
      size = 20
      color = 'red'

    [spectra_layout.xaxis.titlefont]
      family = 'Times new roman, monospace'
      size = 20
      color = 'red'

By simply adding the load_local_config function we can update our plots:

load_local_config('/path/to/your/local_plotting_config.toml')
figure = Plot()
figure1.spectra(wavenumbers, signal, name='an example') 
figure.show()

example passing a local config

easy as that!

This can be done for all three plot types. A complete list of optional layout features can be found in Ploty's documentation for the parent plot type of the three plots currently implemented in this library.

Saving plots

Under the hood, pyet-mc's plotting library leverages Plotly's saving method, therefore it is very simple to save a figure. We provide a save path and file name with the appropriate file extension (e.g. .svg, .pdf for a full list consult the Plotly documentation here)

path = '/path/to/store/'
name = 'file.svg'
figure.save(path, name)

If any errors arise from the plotting, it is again best to consult the Plotly documentation regarding saving figures, as it may require installing the kaleido package separately.

[1] J.L.B. Martin, M.F. Reid, and J-P.R. Wells. Dipole–Quadrupole interactions between Sm³⁺ ions in KY₃F₁₀ nanocrystals. Journal of Alloys and Compounds (2023).

[2] T. Luxbacher, H.P. Fritzer, J.P. Riehl, C.D. Flint. The angular dependence of the multipole–multipole interaction for energy transfer. Theoretical Chemistry Accounts (1999).

[3] T. Luxbacher, H.P. Fritzer, C.D. Flint. Competitive cross-relaxation and energy transfer within the shell model: The case of Cs₂NaSm_xEu_yY_1-x-yCl₆. Journal of Luminescence (1997).

[4] T. Luxbacher, H.P. Fritzer, C.D. Flint. Competitive cross-relaxation and energy transfer in Cs₂NaSm_xEuvGd_1-x-vCl₆. Tunable Solid State Lasers (1997).

Compiling Rust bindings for more stable fitting

Troubleshooting

pyet is using too much memory:
- this is a known issue. Numpy does not seem to free up its arrays fast enough, so it can consume a lot of memory. For example, a 50,000 iteration interaction component and 15,000 time points will consume 6GB of memory. This is why this library does not use pre-allocation, as it is too easy to accidentally run out of memory and use swap memory, slowing things down further. I have a Rust implementation that does not suffer from this issue due to better memory management; This will be part of future releases.
pyet is slow:
- this is also a known issue. This boils down to the number of exponential calls. This is documented here: https://github.com/JaminMartin/pyet-mc/issues/2

The latter two of these issues have been addressed by including Rust bindings described here.

pyet does not converge to a good fit
- This could be for a multitude of reasons. The most probable is either the tolerance for the fit or the fitting algorithm. Try decreasing your tolerance and trying some different methods. Global optimise will soon be available to help remedy the need for good initial guesses. The concentration specified for the interaction component may not be accurate; this, alongside the cross-relaxation parameter being coupled to all traces, may cause an inability to converge. Try to fit with them uncoupled. If you continue to have trouble just reach out! there could be a bug in my code!

Referencing this project

To reference this project, you can use the citation tool in the About info of this repository. Details can also be found in the .cff file in the source code.

License

The project is licensed under the GNU GENERAL PUBLIC LICENSE.

The book of pyet

PYET-MC

A library to model energy transfer between lanthanide ions

Get in contact or follow research related to this project